Simple Functions: Introduction and Basic Optimizations
This blogpost is part of a series of blog posts that discuss different features and optimizations of the simple function interface in Velox.
Introduction to Simple Functions
Scalar functions are one of the most used extension points in Velox. Since Velox is a vectorized engine, by nature functions are "vector functions" that consume Velox vectors (batches of data) and produce vectors. Velox allows users to write functions as vector functions or as single-row operations "simple functions" that are converted to vector functions using template expansion through SimpleFunctionAdapter.
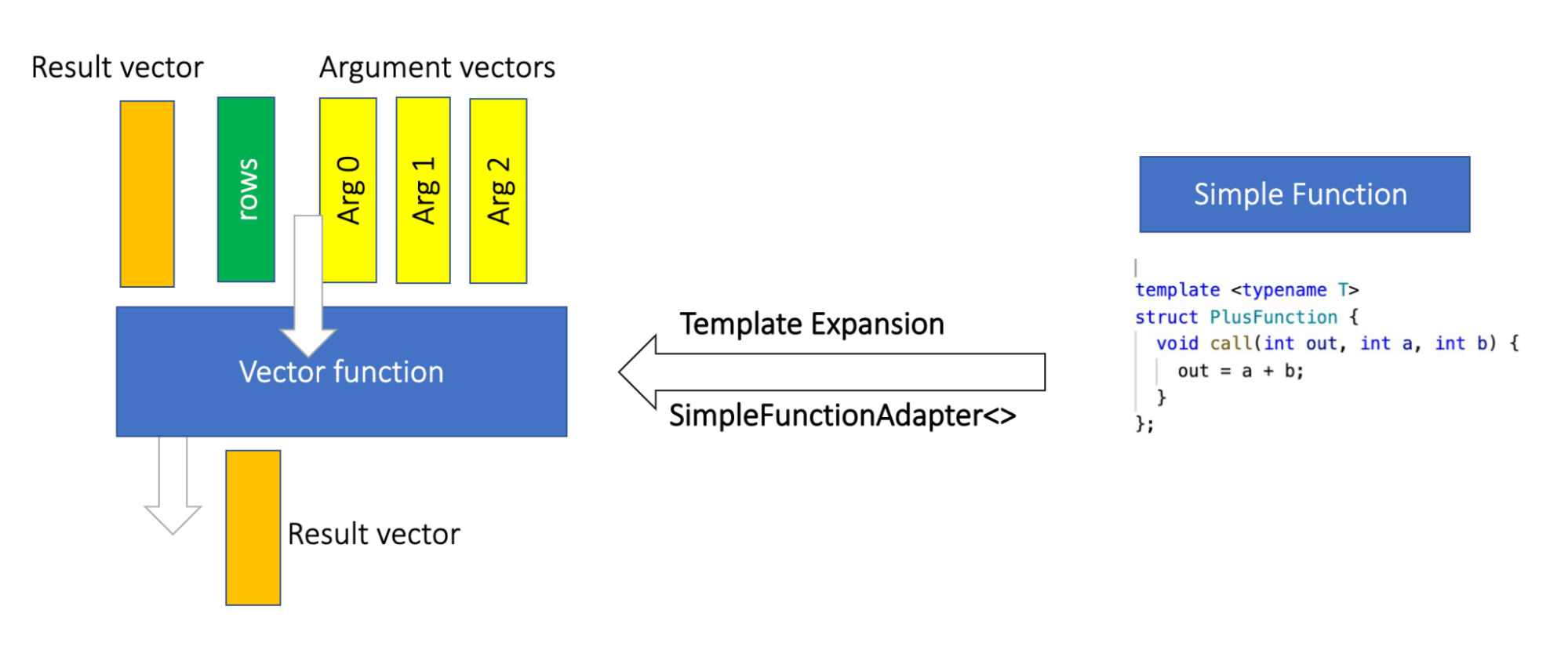
Writing functions as vector functions directly gives the user complete control over the function implementations and optimizations, however it comes with some cost that can be summarized in three points:
- Complexity : Requires an understanding of Velox vectorized data representation and encodings, which requires additional work for our customers, specially those without DB background. Moreover, Writing optimized vector functions requires even deeper understanding.
- Repetition : Involves repeated efforts and code; in each function, authors have to decode the input vectors, apply the same optimizations, and build the output vectors. For example, most arithmetic functions need benefits from a fast path when all the inputs are flat-encoded, authors need to implement that for every function that benefits from it.
- Reliability : More code means more bugs, especially in such a complex context.
Writing functions through the simple interface mitigates the previously mentioned drawbacks, and significantly simplifies the function authoring process. For example, to add the function plus the user only needs to implement the PlusFunction struct shown in the graph above , which is then expanded using template expansion to a vector function.
However, the simple function interface does not give the user full control over the authoring and has its own limitations, for example the function map_keys can be implemented in O(1) as a vector function by moving the keys vector; this is not possible to express as a simple function.
Another limitation is that when using the simple interface, authors do not have access to the encodings of the input vectors, nor control over the encoding of the result vector. Hence, do not have the power to optimize the code for specific input encodings or optimize it by generating specific output encodings. The array_sort function for instance does not need to re-order the elements and copy them during sorting; instead it can generate a dictionary vector as an output, which is something not expressible as a simple function.
In the ideal world we would like to add most of the optimization that someone can do in a vector function to the simple functions adapter, so it would be enabled automatically. We have identified a number of optimizations that apply to all functions and implemented these generically in the SimpleFunctionAdapter. In this way, we can achieve the best of the two worlds and gain Simplicity, Efficiency and Reliability for most functions.
In the past year, we have been working on several improvements to the simple function interface on both the expressivity and performance axes that we will discuss in this series of notes.
In this blog post, we will talk about some of the general optimizations that we have in the adapter, the optimizations discussed in this post make the performance of most simple functions that operates on primitive types matches their counter optimized vector function implementations. In the next blog post, we will discuss complex types in simple functions.
General Optimizations
Vector Reuse
If the output type matches one of the input types, and the input vector is to die after the function invocation, then it is possible to reuse it for the results instead of allocating a new vector. For example, in the expression plus(a, b), if a is stored in a flat vector that is not used after the invocation of the plus function, then that vevtor can be used to store the reults of the computation instead of allocating a new vevtor for the results.
Bulk Null Setting
Nulls are represented in a bit vector, hence, writing each bit can be expensive specially for primitive operations (like plus and minus). One optimization is
to optimize for the not null case, and bulk setting the nulls to not null. After that during the computation, only if the results are null, the null bit is set to null.
Null Setting Avoidance
The adapter can statically infer if a function never generates null; In the simple function interface if the call function return's type is void, it means the output is never null, and if it's bool, then the function returns true for not null and false for null).
When the function does not generate nulls, then null setting is completely avoided during the computation (only the previous bulk setting is needed). The consequence of that is that the hot loop applying the function becomes simdizable triggering a huge boost in performance for primitive operations.
Worth to note also that if the simple function happens to be inlined in the adapter, then even if its return type is not void, but it always returns true then the compiler will be able to infer that setting nulls is never executed and would remove the null setting code.
Encoding Based Fast Path
Vectors in Velox can have different encodings (flat, constant..etc). The generic way of reading a vector of arbitrary encoding is to use a decoded vector to guarantee correct data access. Even though decoded vectors provide a consistent API and make it easier to handle arbitrarily encoded input data, they translate into an overhead each time an input value is accessed (we need to check the encoding of the vector to know how to read the value for every row).
When the function is a primitive operation like plus or minus, such overhead is expensive! To avoid that, encoding based fast paths can be added, the code snippet below illustrates the idea.

In the code above, the overhead of checking the encoding is switched outside the loop that applies the functions (the plus operation here). And the inner loops are simple operations that are potentially simdizable and free of encoding checks.
One issue with this optimization is that the core loop is replicated many times. In general, the numbers of times it will be replicated
is n^m where n is the number of args, and m is the number of encodings.
To avoid code size blowing, we only apply this optimization when all input arguments are primitives and the number of input arguments is <=3. The figure below shows the effect of this optimization on the processing time of a query of primitive operations (the expression is a common pattern in ML use cases).

To compromise for both (performance and code size) when the conditions for specializing for all encodings are not met, we have a pseudo specialization mode that does not blow up the code size, but still reduce the overhead of decoding to a single multiplication per argument. This mode is enabled when all the primitive arguments are either flat or constant. The code below illustrates the idea:

When the input vector is constant we can read the value always from index 0 of the values buffer, and when it is flat we can read it from the index row; this can be achieved by assigning a factor to either 0 or 1 and reducing the decoding operation per row into a multiplication with that factor Note that such a multiplication does not prevent simd. The graph above shows that the psudeo specialization makes the program 1.6X fatser wi, while the complete specialization makes the program 2.5X faster.
ASCII Fast Path
Functions with string inputs can be optimized when the inputs are known to be ascii. For example the length function for ascii strings is the size of the StringView O(1). But for non-ascii inputs the computation is a more complicated O(n) operation.
Users can define a function callAscii() that will be called when all the string input arguments are ascii.

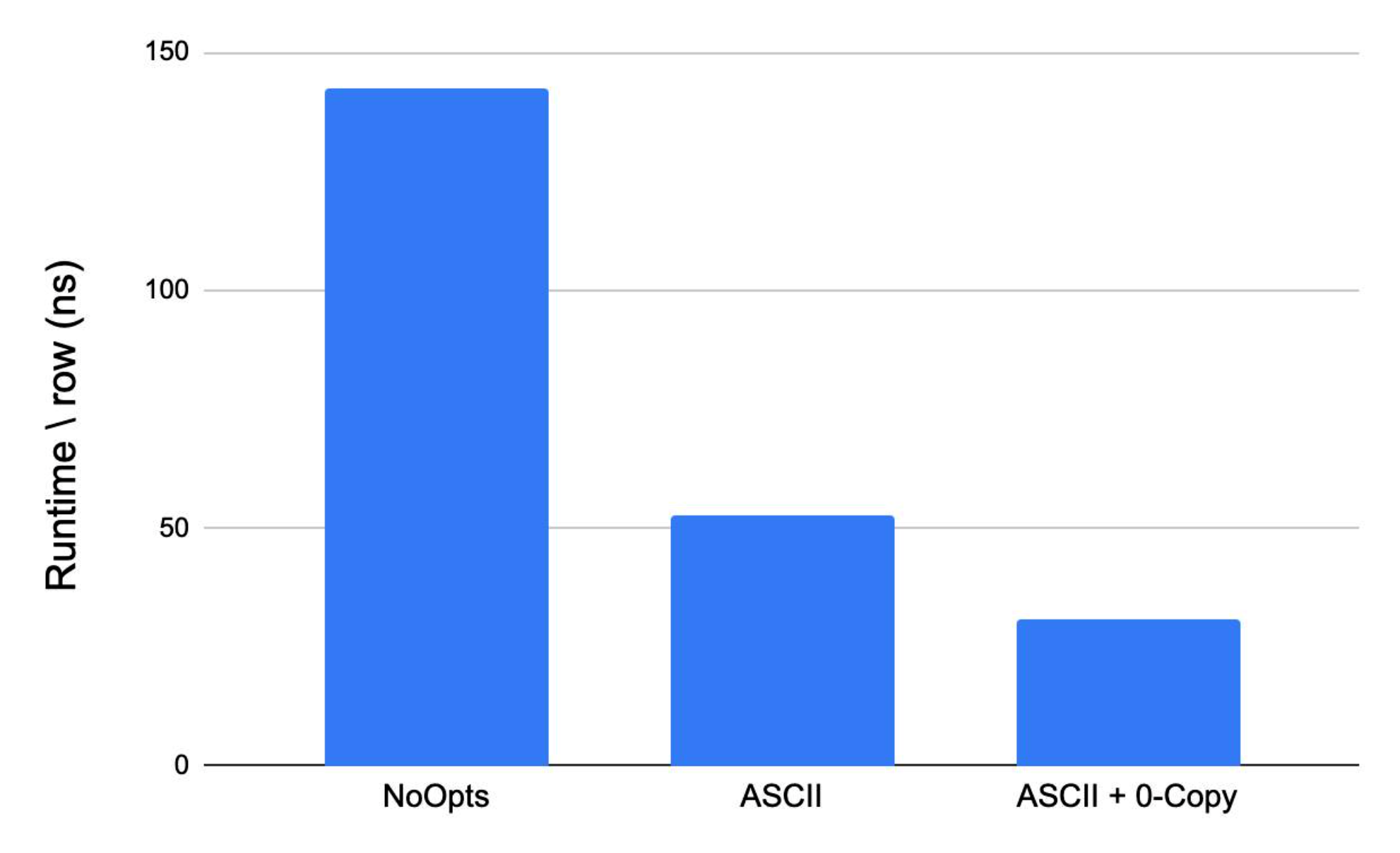
Zero-Copy Optimization
When an input string (or portion of it, reaches the output as is) it does not need to be deep copied. Instead only a StringView needs to be set. Substring is an example of a function that benefits from this. This can be done in the simple function interface in two simple steps.
- Using setNoCopy(); to set the output results without copying string vectors.
- Inform the function to make the output vector share ownership of input string buffers, this can be by setting the field reuse_strings_from_arg.
The graph below shows the effect of the previous two optimizations on the performance of the substring function.
Constant Inputs Pre-processing
Users can pre-process constant inputs of functions to avoid repeated computation by defining initialize function which is called once during query compilations and receives the constant inputs. For example, a regex function with constant pattern would only needs to compile the pattern expressions only once when its constant.
For more information about how to write simple functions check the documentation and the examples.
